What is a Monoidal Category?

This blog post should be accompanied with this post on Hopf algebras, but the order is up to you. At least, I recommend you read them both before proceeding to a couple of my future blog posts where I discuss their connection. Of course, there is plenty of theory one can develop for one object independent from the other. The theory of Hopf algebras and of Tensor Categories is very rich and can be studied independently from each other if the reader wants.

For now, I will definitely assume some familiarity with basic Category Theory. For instance, while most definitions work for arbitrary categories, one commonly considers locally small categories and that is certainly the perspective I will take too.

Another point of order, I am carrying on the unfortunate abuse of terminology in that what I will call a tensor category here is also called a monoidal category. In Etingof, a tensor category is something with far more requirements and structure. However, the origination has ties to actual tensor products of modules, so this is why they were initially called tensor categories. Since I have recently been reading books which prefer the term monoidal, I will do the same. But if I slip up and you find a tensor category anywhere, just let me know and I’ll change it!

Okay, well as the names suggest, whether I call it a monoidal category or tensor category, both of these are founded on the same initial idea of categorification. In the former, one categorifies monoids, while in the latter one considers the categorical properties of the tensor product for \(R\)-modules over a commutative ring and abstracts them. Whichever school of thought you subscribe to, the resulting categorical notion is the same.

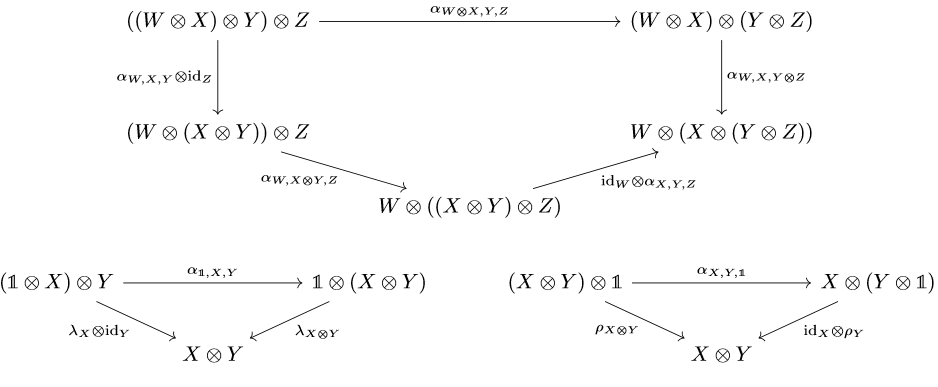
A monoidal category is a sextuple \((\mathcal{C},\otimes,1,\alpha,\rho,\lambda)\) consisting of a (locally small) cateogry \(\mathcal{C}\) with a bifunctor \(\otimes: \mathcal{C}\times\mathcal{C}\to\mathcal{C}\), an object \(1\in\text{Ob}(\mathcal{C})\), and three natural isomorphisms

\begin{equation*} \alpha: \otimes\circ(\otimes\times\text{id}_{\mathcal{C}})\to \otimes\circ(\text{id}_{\mathcal{C}}\times\otimes) \end{equation*} \begin{equation*} \rho: -\otimes 1\to \text{id}_{\mathcal{C}} \end{equation*} \begin{equation*} \lambda: 1\otimes -\to \text{id}_{\mathcal{C}} \end{equation*}

such that the components of the natural isomorphisms make the following diagrams commute

The diagrams are called the pentagon identity and triangle identity for obvious reasons. The bifunctor \(\otimes\) is called the tensor product of \(\mathcal{C}\), the object \(1\) is called the unit object, and the natural isomorphisms \(\alpha,\rho,\lambda\) are called the associatora, the right-unitor, and the left-unitor. There is an equivalent formulation in Etingof that allows one to define a monoidal category as a quintuple, but I prefer this formulation more.

Some examples of monoidal categories include Ab, \(R\)-mod, and \(\textbf{Vec}_{k}\). More deeply, the category of representations of a complex Lie algebra or of a finite group also forms a monoidal category.